Pages by Andreas Hofmeier
 An-H
 eMail Impressum/Note Datenschutzerklärung
http[s]://www.abmh.de/fhs/GRT-L/Bericht/GRT.HTML/index.html
Like to be free? ... then: Fight for Freedom

PDF Version LaTeX SRC

Realisierung einer Drehzahlregelung

Andreas Hofmeier







Auftraggeber: Prof. Dr. Philippsen,
  Fachhochschule Bremen
Ort der Durchführung: FH Bremen, Flughafenallee 10,
  Labor-Platz 5 im Raum 124
Abgabe am: 01.03.2004

Andreas Hofmeier   ___________________







Zusammenfassung:

.
In diesem Versuch ging es darum sich mit den Grundlagen der Regelungstechnik vertraut zu machen. Und das Gelernte auf eine Drehzahlregelung anzuwenden, bei der es darum ging einen Entwurf einer möglichst schnellen Regelstrecke zu erproben. Vorgabe war ein Toleranzband von 5%.
Zum Einsatz kam ein Leybold Versuchsaufbau Motor/Generator verknüpft mit einer elektronischen Strecke als Vorschaltglied.


Inhalt

Versuchsaufbau

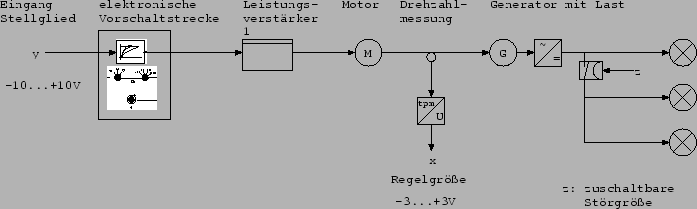
\begin{figure}\centerline{\epsffile{Aufbau.eps}}\end{figure}

Die zu regelnde Strecke bestand aus einem Motor, vor den eine elektronische Strecke geschaltet wurde. Durch die elektronische Strecke wurde die Strecke ``individuell'' gemacht. Die elektronische Strecke wurde auf folgende Werte eingestellt:

$ T = 0.1$
$ d = 2$

Die Messungen wurden an der Strecke auf Labor-Platz 5 im Raum 124 am Standort Flughafenallee 10 durchgeführt.

Die Stellgröße wird zuerst durch die vorgeschaltete elektronische Strecke geführt und anschließend mit Zuhilfenahme eines Treibers (Leistungsverstärkers) auf den Motor gegeben. Der Motor treibt ein Schwungrad und einen Generator an. Der Generator speist bis zu drei Lampen über einen Gleichrichter. Zwei der drei Lampen können mit Hilfe eines TTL-Eingangs zugeschaltet werden. Dies stellt die Störgröße dar. Im ``normalen'' Betrieb ist eine Lampe angeschlossen.

Die Regelgröße ist in diesem Fall die Anzahl der Drehungen pro Minute und wird am Schwungrad gemessen. Zu diesem Zweck sind gleichmäßig licht-aufnehmende und licht-reflektierende Flächen über die Höhe des Schwungrades verteilt. Ein Sensor stellt den Unterschied zwischen den sich abwechselnden Flächen her und sendet bei jeder reflektierenden Fläche einen Impuls. Ein Wandler zählt die Anzahl der Impulse pro Minute und errechnet daraus die Geschwindigkeit bzw. die Ausgangsspannung:

Diese bewegt sich in einem Bereich von $ -3V$ bis $ +3V$, was einer Geschwindigkeit von $ 3000$ Umdrehungen pro Minute in beide Richtungen entspricht. (0V = Stillstand)

Vermessen der Strecke

Statische Kennlinie

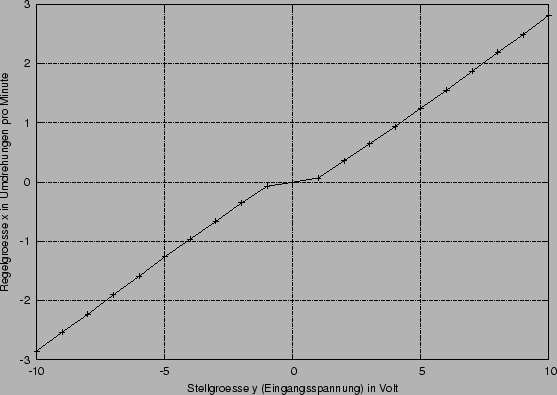
Um einen Überblick über das Streckenverhalten zu erlangen wurde die statische Kennlinie aufgenommen.

[1cm]

[1cm]
y x
0 0,00
1 0,07
2 0,36
3 0,65
4 0,94
5 1,25
6 1,55
7 1,87
8 2,19
9 2,49
10 2,82

y x
0 0,00
-1 -0,07
-2 -0,35
-3 -0,66
-4 -0,96
-5 -1,26
-6 -1,59
-7 -1,9
-8 -2,23
-9 -2,53
-10 -2,85

Die Messungen wurden in der hier aufgeführten Reihenfolge (von oben nach unten, erst links dann rechts) durchgeführt. Die Eingangsspannung $ y$ wurde mit Hilfe eines Potentiometers und eines analogen Multimeters (siehe Geräteliste Seite [*]) eingestellt.

Nach dem sich die Ausgangsspannung ($ x$) auf einen festen Wert eingestellt hatte, wurde dieser abgelesen. Es verging mindestens eine Minute zwischen

einstellen der Eingangsspannung und ablesen der Ausgangsspannung. Die Ausgangsspannung wurde mit Hilfe des in der Geräteliste (siehe Seite [*]) aufgeführten Digitalmultimeters gemessen. Die statische Kennlinie:

\begin{figure}\centerline{\epsffile{statischeKennlinie.eps}}\end{figure}

Sprungantwort

Nun wurde die Sprungantwort der Strecke mit Hilfe der Regelungs- und Simulationssoftware WinFACT/Boris aufgenommen. Diese Software wurde im gesamten weiteren Versuch verwendet und wird daher nicht immer wieder aufgeführt. Hier die ``Schaltung'' innerhalb der Simulationssoftware:

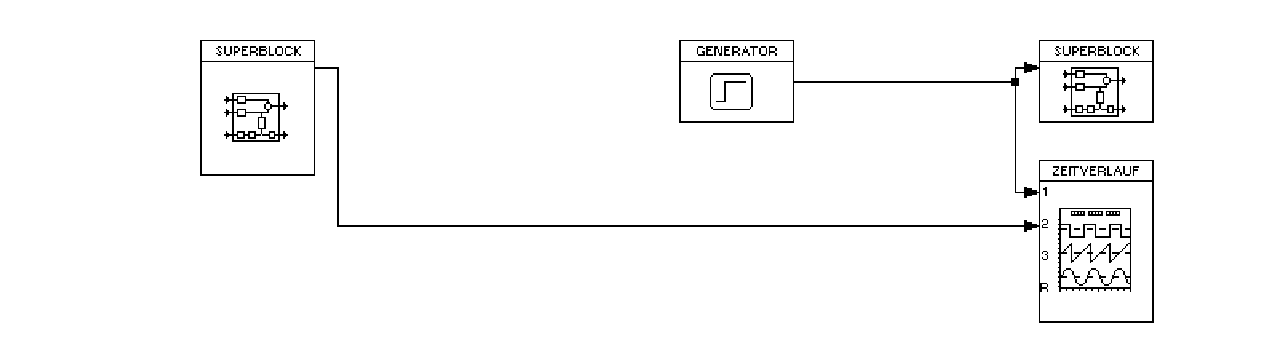
\begin{figure}\centerline{\epsffile{Sprungantwort_BORIS.eps}}\end{figure}

Es wurde folgender Sprung auf die Stellgröße (welche in diesem Fall die Eingangsgröße darstellt) gegeben. (Vor und nach dem Sprung wurde die Eingangsspannung lange genug konstant gehalten):

$ y_{20s - \Delta t} = 5V$
$ y_{20s + \Delta t} = 7V$
$ \Delta t \rightarrow 0$

Reaktion der Regelgröße auf den Sprung:

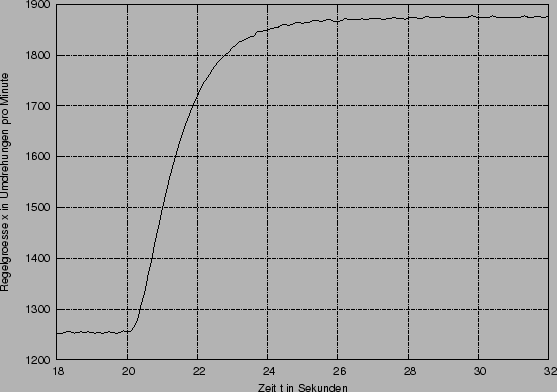
\begin{figure}\centerline{\epsffile{Sprungantwort.eps}}\end{figure}

Ersatzstrecke

Aufbau

Aus der Sprungantwort wurde mit Hilfe dieses Aufbaus die Ersatzstrecke abgeleitet:

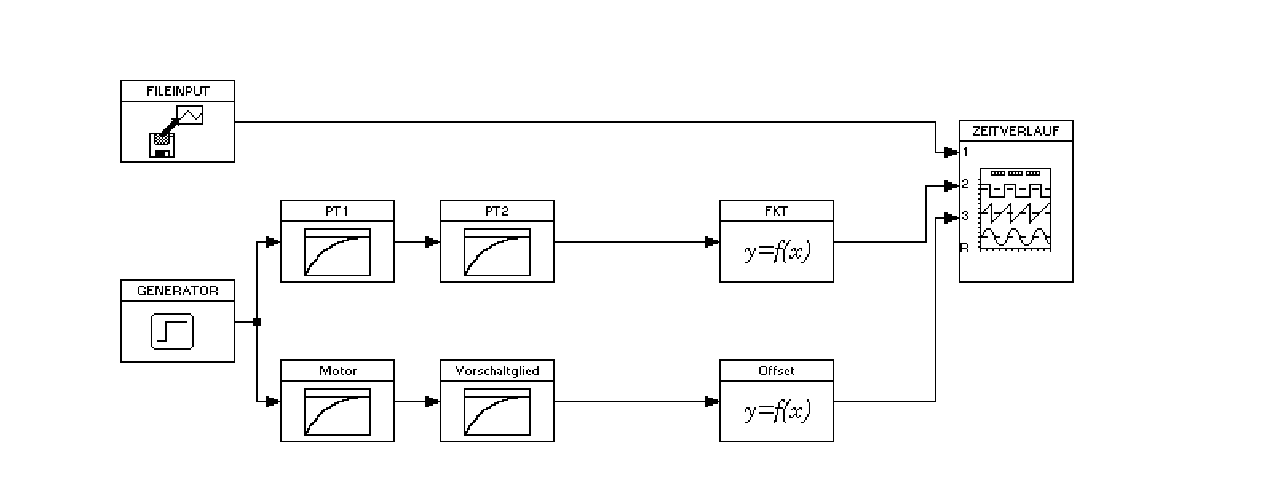
\begin{figure}\centerline{\epsffile{Ersatzstrecke_BORIS.eps}}\end{figure}

Aufnahme der Streckencharakteristiken

Als erstes wurden aus der aufgenommenden Sprungantwort die Streckencharakteristiken entnommen.

(Siehe Seite [*] im Anhang)

$ t_{10} = 0.43s$
$ t_{90} = 3s$

Aus diesen Werten konnte die Ordnung der Strecke errechnet werden:

$ \mu = \frac{t_{10}}{t_{90}} = 0.143 \Rightarrow n = 2$

Die Umwandlung von $ \mu$ in die Ordnung erfolgte durch ablesen einer Tabelle aus dem GRT-Skript. Die Strecke ist laut dieser Rechnung 2. Ordnung. Sie wird also mit zwei hintereinandergeschalteten P-$ T_1$-Gliedern im Computer nachgebildet.

Das die Rechnung eine Ordnung von ``nur'' zwei ergibt ist etwas verwunderlich. Denn die vorgeschaltete elektronische Strecke ist an sich schon mindestens zweiter Ordnung. Hinzu kommt der Montor mit erster Ordnung. Wahrscheinlich sind die weiteren Zeitkonstanten der Ordnungen der vorgeschalteten elektronischen Strecke so klein, dass sie nicht ins Gewicht fallen.

(Siehe Seite [*] im Anhang)

$ T_{\Sigma} = 1.5s$

$ \Delta x = 0.65V$
$ K_s = \frac{\Delta x}{\Delta y} = \frac{0.65V}{2V} = 0.328$

Bestimmung der Parameter der Ersatzstrecke

Diese Werte wurden dann auf die zwei P-$ T_1$-Glieder ``aufgeteilt'', welche die Strecke nachbilden sollten. Das erste stellt den Motor ($ T_1$ und $ K_1$) da und das zweite die vorgeschaltete elektronische Strecke ($ T_2$ und $ K_2$). Die Werte für den Motor waren auf Grund eines vorher durchgeführten Versuches bekannt. Die Parameter für das zweite P-$ T_1$-Glied wurden auf Grund folgender Zusammenhänge errechnet:

$ K_s = K_1 * K_2 \Rightarrow K_2 = \frac{K_s}{K_1}$
$ T_{\Sigma} = T_1 + T_2 \Rightarrow T_2 = T_{\Sigma} - T_1$

Probieren, also das gezielte drehen an diesen Parametern, führte zu folgenden Ergebnissen:

Motor:

$ K_1 = 0.335$
$ T_1 = 1$

P-$ T_1$-Glied (entspricht der vorgeschalteten elektronischen Strecke):

$ K_2 = 0.929$
$ T_2 = 0.58$

$ Offset = -0.305$

mit denen eine nahezu perfekte Simulation der Strecke möglich ist:

Vergleich Strecke und Ersatzstrecke anhand der Sprungantwort

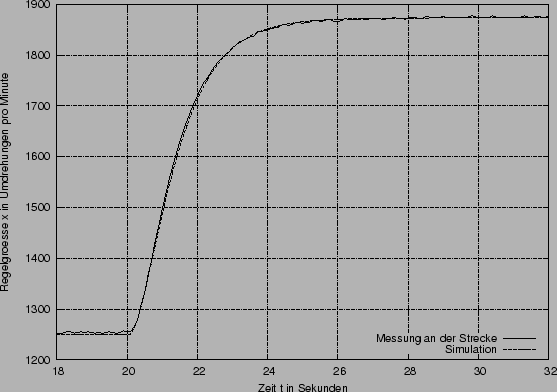
\begin{figure}\centerline{\epsffile{Sprungantwort_ersatz2.eps}}\end{figure}

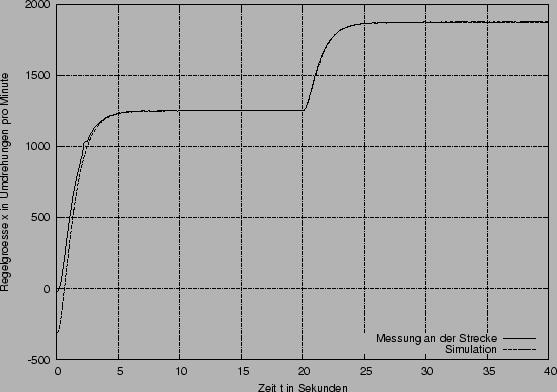
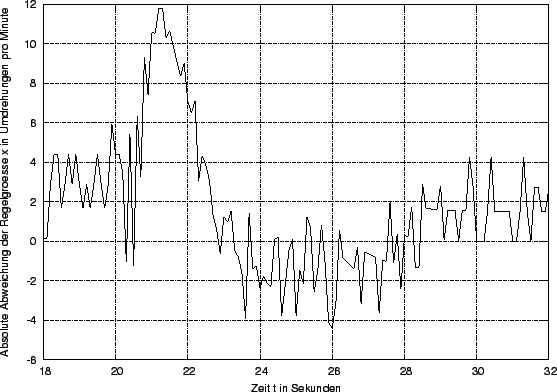
Weitere Betrachtungen: Die maximale Abweichung der Simulation von der Streckensprungantwort beträgt 11.8 Umdrehungen pro Minute. Der Mittelwert der absoluten Abweichung beträgt 1.7 Umdrehungen pro Minute. Rechts ist die absolute Abweichung in Umdrehungen pro Minute über die Zeit in dem betrachtetem Zeitraum von 18 bis 32 Sekunden aufgetragen.

Links sehen Sie den gesamten Verlauf des Versuches zur Aufnahme der Sprungantwort und Ermittlung der Ersatzstrecke.

\begin{figure}\centerline{\epsffile{Sprungantwort_ersatz2_ges.eps}}\end{figure}

\begin{figure}\centerline{\epsffile{Sprungantwort_ersatz2_diff.eps}}\end{figure}

Regelung der Strecke

Aufbau: Simulation

Mit Hilfe dieses Aufbaues wurden die entworfenen Regler im Computer getestet:

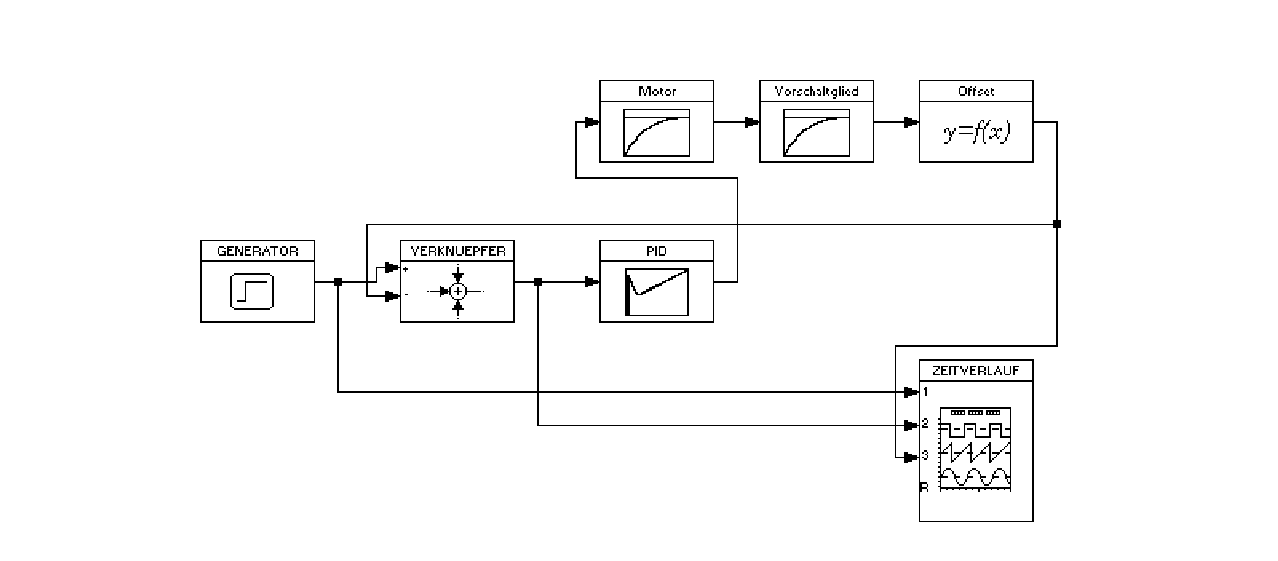
\begin{figure}\centerline{\epsffile{Reglersimulation_BORIS.eps}}\end{figure}

Mit Hilfe des Generators wurde der obligatorische Sprung auf den Regelkreis geschaltet. Eigentlich schaltet er zwei Sprünge auf den Regelkreis:

$ w_{0s - \Delta t} = 0V$
$ w_{0s + \Delta t} = 1V$
$ \Delta t \rightarrow 0$

$ w_{20s - \Delta t} = 1V$
$ w_{20s + \Delta t} = 1.5V$
$ \Delta t \rightarrow 0$

Es handelt sich hier um einen kompletten Regelkreis. Die Regelstrecke (Motor, Vorschaltglied und Offset) ist in diesem Fall die im Abschnitt [*] ab Seite [*] hergeleitete Ersatzstrecke. Als Regler kam der Software-PID-Regler zum Einsatz, in dem die jeweiligen Parameter eingestellt wurden.

Aufbau: Regelung

Mit Hilfe dieses Aufbaus wurden die entworfenen Regler an der realen Strecke getestet:

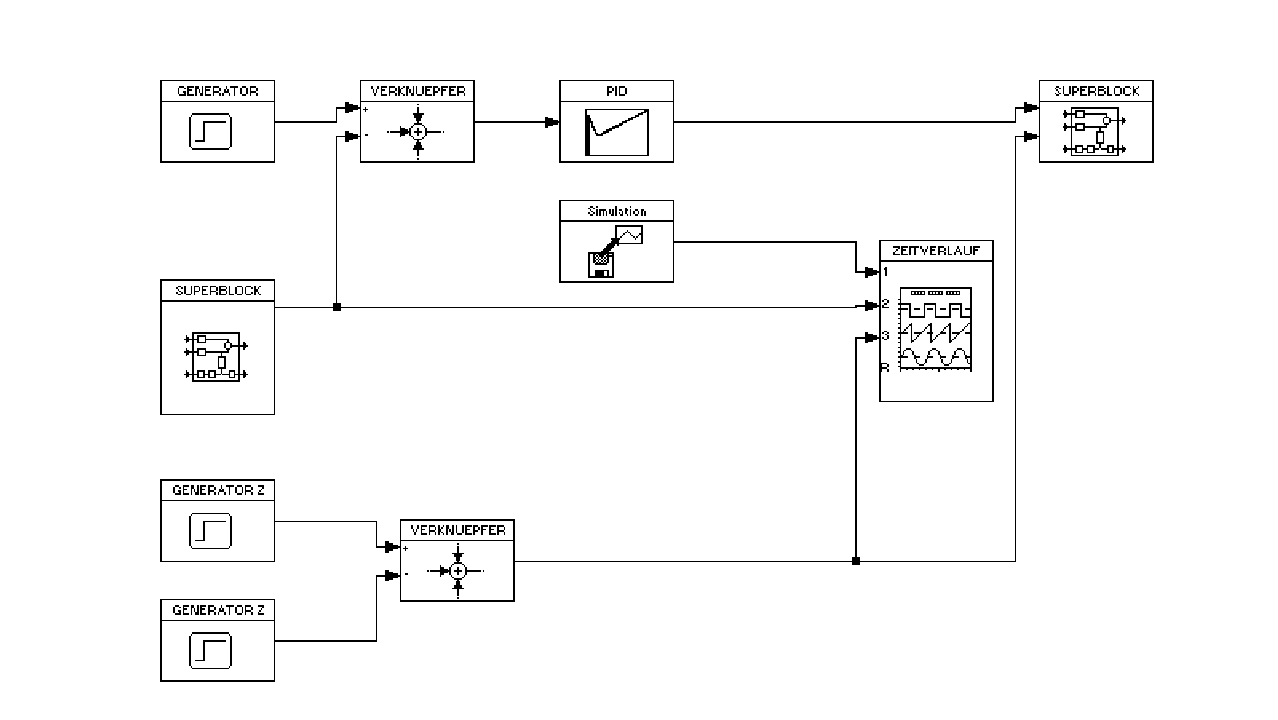
\begin{figure}\centerline{\epsffile{Reglertest_BORIS.eps}}\end{figure}

Mit Hilfe des Generators wurde der obligatorische Sprung auf den Regelkreis geschaltet. Auch hier handelt es sich um einen kompletten Regelkreis, mit dem Unterschied, dass die Regelstrecke diesmal die reale Strecke war. Mit Hilfe von Superblöcken wurde eine Verbindung zum IO-System von Wago realisiert. Das IO-System wurde mit der Strecke verdrahtet. Der Eingang der Strecke ist der Ausgangs der IO-Systems: Superblock rechts. Und umgekehrt.

Die Störungen wurden automatisch über einen weiteren Ausgang des IO-Systems zugeschaltet. Dies wird realisiert, indem die beiden Generatoren ``Generator Z'' jeweils +5V und -5V ausgeben. Zuerst ist keiner der Generatoren aktiv. Die gesamte Ausgangsspannung ist 0V. TTL 0V $ \Rightarrow$ keine Störung. Bei $ t = 40s$ gibt der +5V-Generator Spannung. Die Ausgangsspannung ist nun 5V. TTL 5V $ \Rightarrow$ ``Störung an''. Bei $ t = 60s$ gibt der -5V-Generator ebenfalls Spannung, was zur gegenseitigen Auslöschung der Signale führt. TTL 0V $ \Rightarrow$ ``Störung aus''.

Die Störung wurde wie bereits im Versuchsaufbau beschrieben mit Hilfe der Zuschaltung zweier zusätzlicher Lampen realisiert.

Als Regler kommt der Software-PID-Regler zum Einsatz, in dem die jeweiligen Parameter eingestellt wurden.

Übersicht der Geschehnisse bei dem Reglertest

Zeit t in s Aktion
0 Sprung der Führungsgröße w von 0V auf 1V
20 Sprung der Führungsgröße w von 1V auf 1.5V
40 Störung z (bzw. zwei zusätzliche Lampen) an
60 Störung z (bzw. zwei zusätzliche Lampen) aus
80 Ende des Versuches

In der Simulation war es mir leider nicht möglich die Störungen zu simulieren.

Reglerentwurf, Simulation und Test

Die Formeln zur Errechnung der Reglerparameter und die Regeln zur Ablesung der Werte aus der Sprungantwort wurden alle aus dem GRT-Skript entnommen.

Das Toleranzband beträgt in unserem Fall 5%.

nach $ T_\Sigma$-Regel

Es wurden die bereits ermittelten Streckenparameter in die Formeln für das schnelle Führungsverhalten eingesetzt:

[1cm]

$ K_P = \frac{2}{K_s} = 6.43$
$ T_n = 0.8 T_\Sigma = 1.26$
$ T_v = 0.194 T_\Sigma = 0.307$

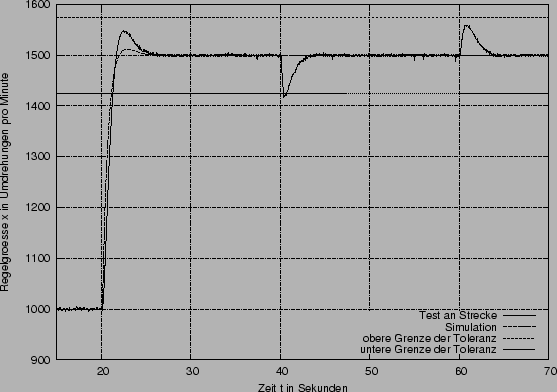
\begin{figure}\centerline{\epsffile{Regler_ts_ges.eps}}\end{figure}

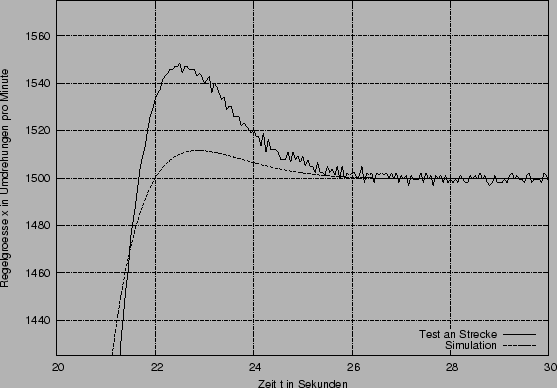
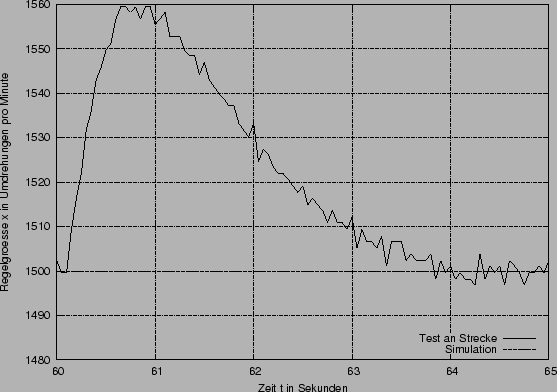
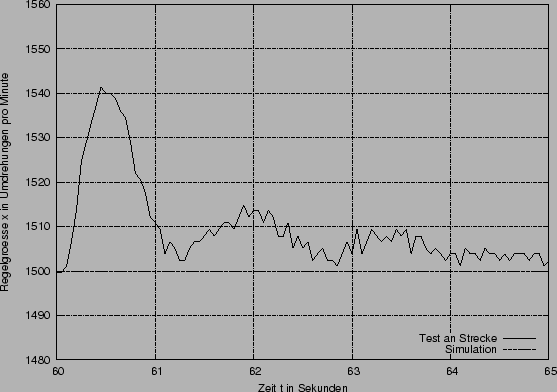
Der obere Graph zeigt den Verlauf der zweiten Sprungantwort (Sprung der Führungsgröße w von von 1V auf 1.5V, also 1000 auf 1500 Umdrehungen pro Minute) und der An- und Abschaltung der Last. Unten links sehen sie den Verlauf der Regelgröße bei dem zweiten Sprung. Die Diagrammgrenzen der Regelgröße entsprechen dem Tolereanzband von 5%. Diese Diagrammgrenzen werden im weiteren bei der Darstellung der zweite Sprungantwort beibehalten. Rechts ist die Abschaltung der Last dargestellt.

\begin{figure}\centerline{\epsffile{Regler_ts_spr.eps}}\end{figure}

\begin{figure}\centerline{\epsffile{Regler_ts_str.eps}}\end{figure}

nach Chien, Hrones und Reswick

Für dies Einstellregel mussten zusätzliche Streckenwerte durch anlegen der Tangente abgelesen werden (Siehe Seite [*] im Anhang). Es wurde die Regel für schnelles Führungsverhalten für den PID-Regler angewendet.

[1cm]

$ T_u = 0.24$
$ T_G = 1.96$

$ K_p = 0.95 \frac{T_G}{T_u K_s} = 24.9$
$ T_n = 1.35 T_G = 2.65$
$ T_v = 0.47 T_u = 0.113$

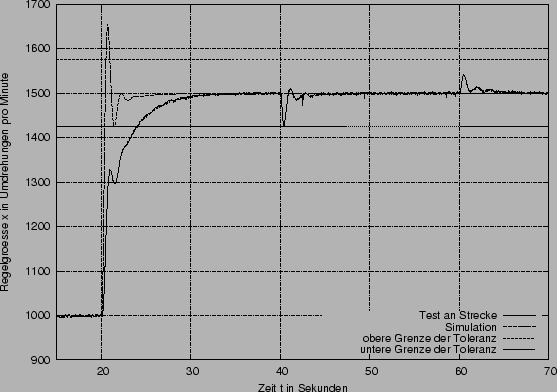
\begin{figure}\centerline{\epsffile{Regler_chrs_ges.eps}}\end{figure}

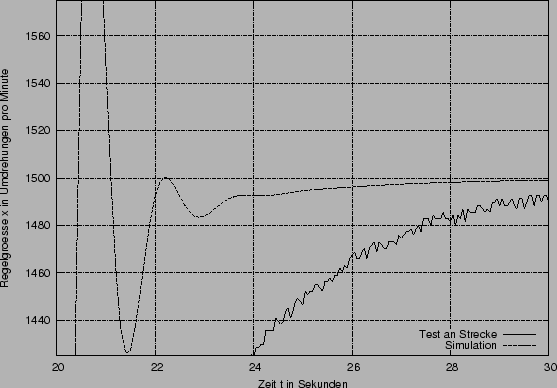
\begin{figure}\centerline{\epsffile{Regler_chrs_spr.eps}}\end{figure}

\begin{figure}\centerline{\epsffile{Regler_chrs_str.eps}}\end{figure}

Interessant ist hier die Abweichung des simulierten Verhaltens von dem tatsächlichen: Im Gegensatz zur $ T_\Sigma$-Regel kommt es hier bei dem zweiten Führungssprung zu einem erheblichen Überschwingen der simulierten Strecke. Während bei der $ T_\Sigma$-Regel das reale Verhalten besser vorhergesagt wurde und das Überschwingen der Simulation kleiner war.

theoretischer Reglerentwurf

Bei dem theoretischen Reglerentwurf für den PID-Regler werden die zwei größten Zeitkonstanten der Strecke kompensiert:

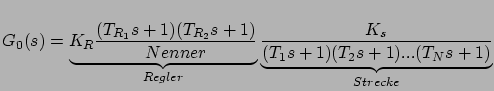
$ G_0(s) = \underbrace{K_R \frac{(T_{R_1}s + 1)(T_{R_2}s + 1)}{Nenner}}_{Regler} \underbrace{\frac{K_s}{(T_1 s + 1)(T_2 s + 1) ... (T_N s + 1)}}_{Strecke}$

Ich nehme an, dass $ T_1$ und $ T_2$ die größten Zeitkonstanten sind. So muss man lediglich dafür sorgen, dass $ T_{R_1} = T_1$ und $ T_{R_2} = T_2$ gilt. Dann kürzen sich diese Zeitkonstanten weg.

Durch geschicktes umformen kann die Parameter des PID-Reglers aus $ T_1$ und $ T_2$ entnehmen:

$ T_N = T_1 + T_2 = 1.58$
$ T_v = \frac{T_1 * T_2}{T_1 + T_2} = 0.367$

Für die beiden größten Zeitkonstanten habe ich die zwei mir bekannten gewählt:

$ T_1 = 1$ (Motor)
$ T_2 = 0.58$ (elektronische Strecke)

Für die Berechnung der optimalen Reglerverstärkung aufgrund der maximalen Überschwingweite sind die restlichen Zeitkonstanten der Strecke erforderlich. Da diese nicht zu Verfügung standen, wurde die bei der $ T_\Sigma$-Regel gefundene Reglerverstärkung verwendet.

$ K_p = 6.43$

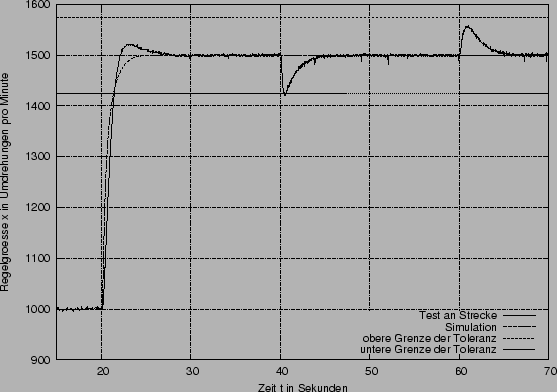
\begin{figure}\centerline{\epsffile{Regler_ent_ges.eps}}\end{figure}

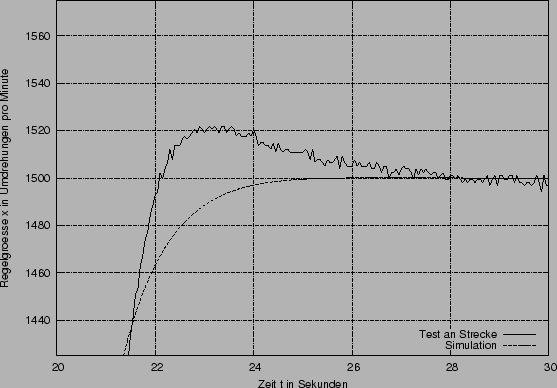
\begin{figure}\centerline{\epsffile{Regler_ent_spr.eps}}\end{figure}

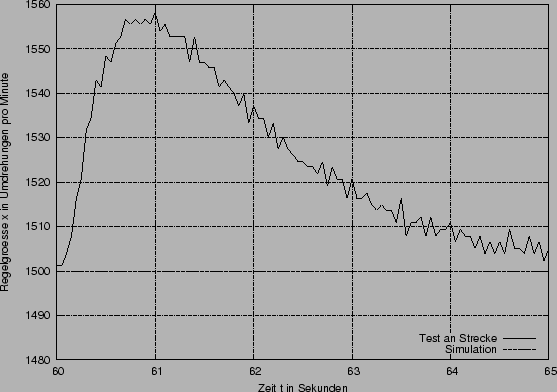
\begin{figure}\centerline{\epsffile{Regler_ent_str.eps}}\end{figure}

Interessant ist hier die Abweichung des simulierten Verhaltens von dem tatsächlichen: Bei der Simulation kam es zu keinem Überschwinger beim zweiten Führungssprung, während die reale Strecke einen Überschwinger verursacht.

Vergleich der Regler

Führungsverhalten

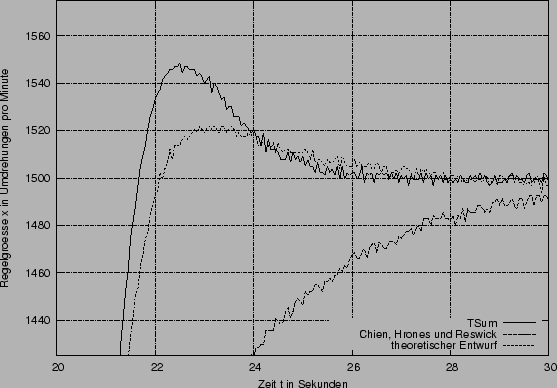
\begin{figure}\centerline{\epsffile{Regler_Vergl_spr.eps}}\end{figure}

  $ T_\Sigma$ Chien Hrones Reswick theoretischer Entwurf
Überschwingweite 50 0 20
Anregelzeit 1.3s 4s 1.5s
Ausregelzeit 1.3s 4s 1.5s

Da ein Regler mit I-Anteil mit einer $ PT_N$-Strecke zum Einsatz kam wurde stationäre Genauigkeit erreicht.

In diesem Fall ist für mich der theoretische Reglerentwurf der Sieger. Wenn allerdings die Überschwingweite innerhalb des Toleranzbandes unberücksichtigt bleiben soll, so ist der nach $ T_\Sigma$-Regel entworfene Regler der beste, da er am schnellsten ausregelt. Durch einstellen der Reglerverstärkung hätte der theoretische Reglerentwurf schneller oder langsamer gemacht werden können. Je schneller der Regler ist, desto größer ist leider auch die Überschwingweite.

Nach einem ``kleinen Überschwinger'' regelten der theoretische und der $ T_\Sigma$-Regler die Störung in einem aperiodischen Grenzfall-ähnlichen Verlauf aus. Der Chien, Hrones und Reswick-Regler durchläuft, bis auf einen kleinen ``Schwinger'', einen aperiodischen Grenzfall-ähnlichen Verlauf. Er ist der langsamste Regler. Allerdings verursacht er keinen Überschwinger.

Störverhalten

Zuschalten der Last (zwei zusätzliche Lampen):

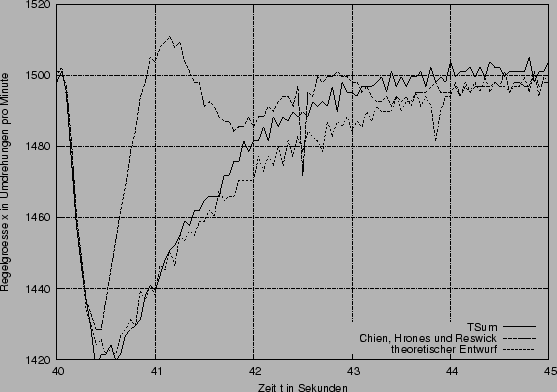
\begin{figure}\centerline{\epsffile{Regler_Vergl_str2.eps}}\end{figure}

Abschalten der Last:

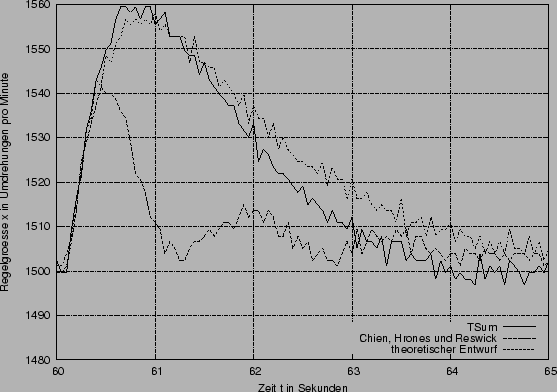
\begin{figure}\centerline{\epsffile{Regler_Vergl_str.eps}}\end{figure}

Störung die durch das Zuschalten der Last (zwei zusätzliche Lampen) verursacht wird:

  $ T_\Sigma$ Chien Hrones Reswick theoretischer Entwurf
Überschwingweite -82 -70 -77
Zeit bis $ \Delta x \approx 0$ 3.5s 5s 5s

Störung die durch das Abschalten der Last verursacht wird:

  $ T_\Sigma$ Chien Hrones Reswick theoretischer Entwurf
Überschwingweite 60 40 58
Zeit bis $ \Delta x \approx 0$ 4s 4.5s 5.5s

Deutlich zu erkennen ist, dass bei der Zuschaltung der Last eine deutlich größere Störung verursacht wird, als bei dem Abschalten. Dies Zuschalten führt zu einer Bremsung durch die Last am Generator und verlässt sogar kurz das Toleranzband von 5%. Diese Bremsung äußert sich im Sinken der Drehgeschwindigkeit, also einem absinken der Regelgröße. Dieses Absinken ist natürlich nur von kurzen Dauer, da der Regler die Störung ausregelt.

Beim wiederabschalten die Last wird die Bremse sozusagen gelöst, was im ersten Moment zu einer Beschleunigung führt.

Deutlich zu erkennen ist, dass der nach Chien, Hrones und Reswick eingestellte Regler zu Schwingungen neigt. Seine Überschwingweite ist allerdings auch am kleinsten. Die beiden anderen Regler $ T_\Sigma$ und theoretischer Reglerentwurf verhalten sich ähnlich. Nach einem Überschwinger (durch die Störung verursacht) lenken sie die Regelgröße in einem aperiodischen Grenzfall-ähnlichen Verlauf auf den Sollwert zurück.

In diesem Fall ist der $ T_\Sigma$-Regler der klare Sieger, denn er regelt am schnellsten innerhalb des Toleranzbandes aus. Er ist etwas schneller als der theoretisch entworfene Regler, allerdings schwingt er etwas mehr über. Durch ``herumdrehen'' an der Reglerverstärkung hätte man den theoretisch entworfenen Regler noch erheblich schneller machen können. So hätte dieser den $ T_\Sigma$-Regler schlagen können. Die Verstärkung stellt die Geschwindigkeit, allerdings auch die Überschwingweite, ein. Aus bereits erwähnten Gründen war eine theoretische Berechnung der Reglerverstärkung leider nicht möglich.

Anhang

Geräteliste

Gerät Hersteller Typ Toleranz
Analoges Multimeter Siemens Multizet $ \pm 1.5\%$
Digitales Multimeter Fluke 75  
Stabilisiertes Netzteil $ \pm$ 15V/3A Leybold 726 86  
Führungsgrößengeber Leybold 734 02  
Übertragungsglied 2. Ordnung Leybold 734 059  
Leistungsverstärker Leybold 734 13  
Motor Generatorsatz, 24V, 3000 $ \frac{U}{min}$, 3.8W Leybold 734 11  
Lastschalter Leybold 734 39  
IO-System Wago 750-842 ca. $ \pm 0.1\%$
IO-S.-Netzteil Wago 787-912  
PC      
Drucker HP Deskjet 500  

Quellen

Als Quellen für diesen Bericht dienten die Vorlesung Grundlagen Regelungstechnik im Semester I3.2 WS 2003/2004 an der Hochschule Bremen bei Dr. Philippsen, sowie die dazugehörige Laborveranstaltung und das Skript.


Sprungantwort, Auslesen ($ T_\Sigma$, $ K_s$) mit Hilfe von TSum-Regel


Sprungantwort, Auslesen ($ \mu$, $ t_u$, $ t_G$) nach Chien Hrones Reswick

PDF Version LaTeX SRC

Pages by Andreas Hofmeier
 An-H
 eMail Impressum/Note Datenschutzerklärung
http[s]://www.abmh.de/fhs/GRT-L/Bericht/GRT.HTML/index.html
Creative Commons License
(c) Andreas B. M. Hofmeier
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 Germany License